Definice: O zobrazení Z: X → X' řekneme, že je to
zobrazení podobné, jestliže existuje kladné reálné číslo k
tak, že obrazem každé úsečky AB je úsečka A'B', pro
kterou platí |A'B'| = k·|AB|. Číslo k nazýváme koeficient
podobnosti.
Věta: Shodné zobrazení je jednoznačně zadané třemi
různými nekolineárními body a jejich obrazy.
Poznámka: Obrazy bodů musí samozřejmě splňovat požadavky pro podobné zobrazení. Trojúhelník určený obrazy bodů musí být podobný trojúhelníku, který určují vzory bodů.
Důkaz: Zvolíme tři nekolineární body A, B, C. Dále k nim vhodně zvolíme jejich obrazy A', B', C' tak, aby platilo: |AB| = k·|A'B'|, |BC| = k·|B'C'|, |AC| = k·|A'C'|, kde k je kladné reálné číslo. Zvolíme libovolný bod D a zjistíme, jestli lze najít jednoznačně jeho obraz D'.
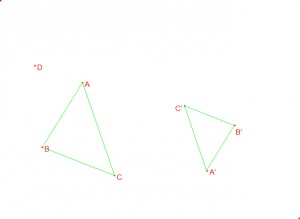
Věta: Každé podobné zobrazení je prosté.
Důkaz: Máme ukázat, že obrazem dvou různých bodů X, Y jsou dva různé body X', Y'. Víme, že platí vztah |X'Y'| = k·|XY|. Body X, Y jsou různé, a proto je velikost úsečky XY nenulová. Koeficient k je podle definice podobného zobrazení také nenulový. Součin dvou nenulových čísel je číslo nenulové. Z toho plyne, že vzdálenost bodů X'Y' je nenulová a body X', Y' jsou tedy různé.
Tvrzení: V podobném zobrazení platí:
Obrazem přímky je přímka; obrazem kružnice je kružnice; obrazem polopřímky je polopřímka, jejíž počáteční bod je obrazem počátečního bodu vzoru polopřímky; obrazem úsečky je úsečka.
Podobné zobrazení s koeficientem k = 1 je shodné zobrazení. Tvrzení ihned plyne z definice shodného a podobného zobrazení. Také platí, že každé shodné zobrazení je podobné zobrazení s koeficientem podobnosti k = 1.
V kapitole o shodných zobrazeních jsme zavedli pojmy přímo a nepřímo shodný trojúhelník jednak pomocí přesouvání trojúhelníků v rovině a také pomocí představy lávek. Pro zavedení pojmu přímo a nepřímo podobný trojúhelník použijeme téměř stejnou představu lávek, kterou již známe, jen trojúhelníky, které lávky tvoří, nejsou shodné, ale podobné. Pokud tedy chodíme po trojúhelnících z lávek s očíslovanými vrcholy, a zahýbáme ve vrcholech obou trojúhelníků vpravo či v obou vlevo, jsou trojúhelníky přímo podobné. Pokud zahýbáme v jednom vpravo a v jednom vlevo, jsou trojúhelníky nepřímo podobné.
Definice: Podobnost, ve které jsou obraz a vzor
trojúhelníku přímo podobné nazveme přímou podobností.
Podobnost, ve které jsou obraz a vzor trojúhelníku nepřímo
podobné nazveme nepřímou podobností.
Příklad 3.1
Je dáno podobné zobrazení s koeficientem podobnosti k a trojúhelník ABC, který má obsah S. Jaký obsah má trojúhelník A'B'C', který je obrazem trojúhelníku ABC v daném podobném zobrazení?
Řešení
Obsah trojúhelníku ABC spočítáme podle vzorce S = |AB|·vAB, kde vAB je výška na
stranu AB.
Obsah trojúhelníku A'B'C' spočítáme podle vzorce S' = |A'B'|·v'A'B', kde v'A'B' je výška na
stranu A'B'.
Úsečky A'B', v'A'B' jsou obrazy úseček AB, vAB v podobném zobrazení s koeficientem k,
a proto mají velikost |A'B'| = k·|AB|, |v'A'B'| = k·|vAB|.
Vyjádříme obsah S' trojúhelníku A'B'C' pomocí obsahu S trojúhelníku ABC.
S' = |A'B'|·v'A'B'
S' = k·|AB|·k·vAB
S' = k2·|AB|·vAB
S' = k2·S
Obsah ΔABC je k2-násobkem obsahu ΔA'B'C'.
Tvrzení: Obsah S' obrazu U' útvaru U s obsahem S v
podobném zobrazení s koeficientem k je k2-násobkem
obsahu S. Tedy platí S' = k2·S.
Komentáře
Přehled komentářů
Welcome to the world of adult Dating loveawake.ru
Wut
(Adri, 10. 12. 2021 22:27)
Já to jakože vůbec nechápu nestačilo by to
napsat jednodušejc?
0
(Peter, 31. 3. 2020 9:54)
Z tohto sa vôbec nedá nič naučiť,vy by ste nemohli vyučovať na školách.
Ďakujem
Blood pressure - If you fancy distinguish more
(AVamimmeda, 8. 10. 2018 23:46)
Torsion bras de quelqu'un est comment poupe votre sang pousse contre les parois de vos arteres lorsque votre coeur essence pompe le sang. Arteres sont les tubes qui transportent perseverent b gerer offre sang loin de votre coeur. Chaque temps votre determination bat, il pompe le sang par de vos arteres a la vacances de votre corps.
https://www.cialispascherfr24.com/tadalafil-100mg-pas-cher-paris/
Re: Blood pressure - If you fancy distinguish more
(Annonymous, 3. 4. 2019 23:28)Chill the *uck down. This is blog, not some free advertisement place.
asd
(blbci, 8. 4. 2010 8:55)je to tady nanic vubec sem to po vas nepochpil...jinak tadu je uzitecny odkaz http://1kspa.cz/kladno/stud_materialy/matematika/Podobnost_trojuhelniku.pdf
BLBOST
(mg, 14. 4. 2015 19:04)taková nehorázná krávovina, většině z nás to bude úplně k hovnu :D
.
(Lucka, 6. 4. 2014 17:20)
Hodně nepřehledně napsané.
Myslím si,že by to šlo mnohem stručněji.Zbytečné.
Zakladka
(DarkAcer, 20. 2. 2014 18:30)
Omg ja to nechapu a to ztoho zejtra píšem..:/
Trošku to prosím upravte.
:D
(Soňa, 17. 2. 2014 9:06)
Je to fakt "krásně a přehledně" napsané :DD
Vůbec se v tom nevyznám,ale asi nejsem jediná, jak tak vidím...
:D
(Soňa, 17. 2. 2014 9:05)
Je to fakt "krásně a přehledně" napsané :DD
Vůbec se v tom nevyznám,ale asi nejsem jediná, jak tak vidím...
Are you 18? Come in and don't be shy!
(loveawake.ru, 21. 1. 2022 16:59)