Definice: O zobrazení Z: X → X' řekneme, že je to
zobrazení podobné, jestliže existuje kladné reálné číslo k
tak, že obrazem každé úsečky AB je úsečka A'B', pro
kterou platí |A'B'| = k·|AB|. Číslo k nazýváme koeficient
podobnosti.
Věta: Shodné zobrazení je jednoznačně zadané třemi
různými nekolineárními body a jejich obrazy.
Poznámka: Obrazy bodů musí samozřejmě splňovat požadavky pro podobné zobrazení. Trojúhelník určený obrazy bodů musí být podobný trojúhelníku, který určují vzory bodů.
Důkaz: Zvolíme tři nekolineární body A, B, C. Dále k nim vhodně zvolíme jejich obrazy A', B', C' tak, aby platilo: |AB| = k·|A'B'|, |BC| = k·|B'C'|, |AC| = k·|A'C'|, kde k je kladné reálné číslo. Zvolíme libovolný bod D a zjistíme, jestli lze najít jednoznačně jeho obraz D'.
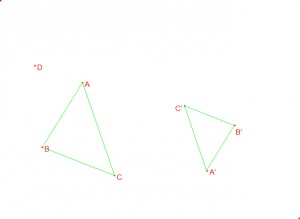
Věta: Každé podobné zobrazení je prosté.
Důkaz: Máme ukázat, že obrazem dvou různých bodů X, Y jsou dva různé body X', Y'. Víme, že platí vztah |X'Y'| = k·|XY|. Body X, Y jsou různé, a proto je velikost úsečky XY nenulová. Koeficient k je podle definice podobného zobrazení také nenulový. Součin dvou nenulových čísel je číslo nenulové. Z toho plyne, že vzdálenost bodů X'Y' je nenulová a body X', Y' jsou tedy různé.
Tvrzení: V podobném zobrazení platí:
Obrazem přímky je přímka; obrazem kružnice je kružnice; obrazem polopřímky je polopřímka, jejíž počáteční bod je obrazem počátečního bodu vzoru polopřímky; obrazem úsečky je úsečka.
Podobné zobrazení s koeficientem k = 1 je shodné zobrazení. Tvrzení ihned plyne z definice shodného a podobného zobrazení. Také platí, že každé shodné zobrazení je podobné zobrazení s koeficientem podobnosti k = 1.
V kapitole o shodných zobrazeních jsme zavedli pojmy přímo a nepřímo shodný trojúhelník jednak pomocí přesouvání trojúhelníků v rovině a také pomocí představy lávek. Pro zavedení pojmu přímo a nepřímo podobný trojúhelník použijeme téměř stejnou představu lávek, kterou již známe, jen trojúhelníky, které lávky tvoří, nejsou shodné, ale podobné. Pokud tedy chodíme po trojúhelnících z lávek s očíslovanými vrcholy, a zahýbáme ve vrcholech obou trojúhelníků vpravo či v obou vlevo, jsou trojúhelníky přímo podobné. Pokud zahýbáme v jednom vpravo a v jednom vlevo, jsou trojúhelníky nepřímo podobné.
Definice: Podobnost, ve které jsou obraz a vzor
trojúhelníku přímo podobné nazveme přímou podobností.
Podobnost, ve které jsou obraz a vzor trojúhelníku nepřímo
podobné nazveme nepřímou podobností.
Příklad 3.1
Je dáno podobné zobrazení s koeficientem podobnosti k a trojúhelník ABC, který má obsah S. Jaký obsah má trojúhelník A'B'C', který je obrazem trojúhelníku ABC v daném podobném zobrazení?
Řešení
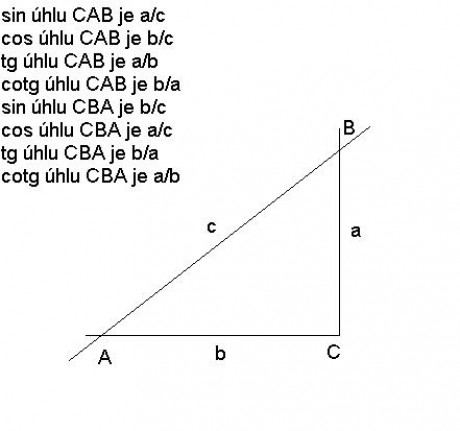
Obsah trojúhelníku ABC spočítáme podle vzorce S = |AB|·vAB, kde vAB je výška na
stranu AB.
Obsah trojúhelníku A'B'C' spočítáme podle vzorce S' = |A'B'|·v'A'B', kde v'A'B' je výška na
stranu A'B'.
Úsečky A'B', v'A'B' jsou obrazy úseček AB, vAB v podobném zobrazení s koeficientem k,
a proto mají velikost |A'B'| = k·|AB|, |v'A'B'| = k·|vAB|.
Vyjádříme obsah S' trojúhelníku A'B'C' pomocí obsahu S trojúhelníku ABC.
S' = |A'B'|·v'A'B'
S' = k·|AB|·k·vAB
S' = k2·|AB|·vAB
S' = k2·S
Obsah ΔABC je k2-násobkem obsahu ΔA'B'C'.
Tvrzení: Obsah S' obrazu U' útvaru U s obsahem S v
podobném zobrazení s koeficientem k je k2-násobkem
obsahu S. Tedy platí S' = k2·S.
Komentáře
Přehled komentářů
Krucii nechápu too:((
Chyba
(parez, 16. 6. 2011 14:06)pěkný, akorát obsah trojúhelníku je S = |AB|.vAB / 2 a ne to co tvrdí autor.
Zbytečně složitě
(anonym, 25. 11. 2010 15:23)Ten článek je napsaný pěkně, ale jako by to bylo ze skript na vysoké škole. Přitom podobnost trojúhelníků se učí lidi na základce, takže je asi zbytečné takhle jim komplikovat život.
hfsliasugfaukgfk
(ladam, 4. 2. 2010 10:47)
Já to taky nechápu, takže buďte všichni v pohodě
...
(Lila, 26. 10. 2011 17:39)