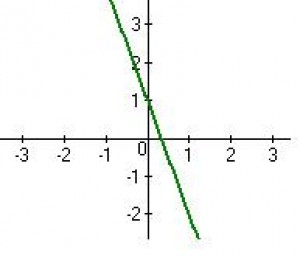
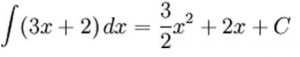- grafem lineární funkce je přímka (ovšem není rovnoběžná se žádnou z os x a y)
- lineární funkce jsou uzavřené na skládání
- lineární funkce není ohraničená ani periodická
- pro k > 0 je lineární funkce rostoucí, pro k < 0 je klesající
- lineární funkce je spojitá
- pro q = 0 prochází počátkem a v takovém případě je lichou funkcí
- lineární funkce má v každém bodě derivaci, která je rovna její směrnici
- primitivní funkce k lineární funkci je kvadratická funkce
ax + b = 0
Přímka je s osou x různoběžná. To nastane v případě, že rovnice přímky jde vyjádřit ve tvaru y = ax + b, pro a nenulové. Tehdy má přímka s osou x jeden průsečík a rovnice má jedno řešení.
- příklad: Určete, zda se jedná o funkci:
|
x
|
–8
|
–7
|
–2
|
–1
|
0
|
–2
|
4
|
6
|
|
f(x)
|
2
|
–5
|
–2
|
2
|
3
|
5
|
2
|
0
|
- příklad: Určete, zda se jedná o funkci:
|
x
|
–7
|
–5
|
–3
|
–1
|
0
|
1
|
2
|
3
|
4
|
|
f(x)
|
–9
|
–7
|
–5
|
–3
|
–1
|
3
|
4
|
5
|
6
|
- příklad: Sestrojte graf funkce y = 3x – 2, jestliže definiční obor této funkce je:
- příklad: Sestroj graf funkce y = 3x – 2, jestliže definiční obor této funkce je:
Řešení k č.1: Tabulkou není určena funkce. Pro x = –2 máme dvě funkční hodnoty, což je v rozporu s definicí funkce.
Řešení k č.2: Tabulka určuje funkci, neboť každému bodu definičního oboru je přiřazena právě jedna funkční hodnota.
|
x
|
–5
|
–4
|
–2
|
0
|
2
|
3
|
5
|
|
f(x)
|
–17
|
–14
|
–8
|
–2
|
4
|
7
|
13
|
Řešení k č.4: Grafem bude úsečka s krajními body [–5; –17] a [5; 13], neboť definiční obor jsou všechna reálná čísla od –5 do 5.